Derivative in form of dy/dx
As Know derivative is all about changes so it actually tells how rapidly something rate change at any point
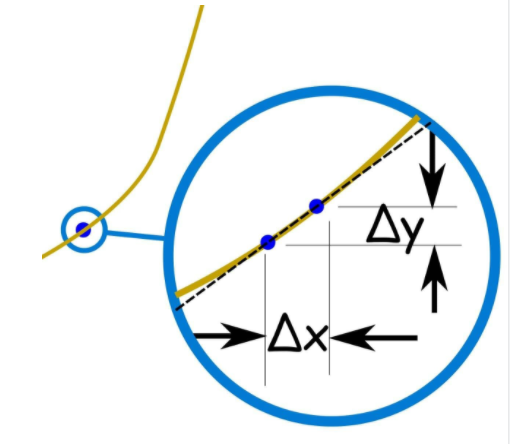
Leibnize Notation
$$\frac{dy}{dx}$$ We start with a function:
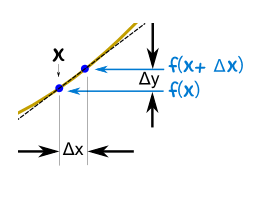
$$Y=f(x).....(a)$$ Step-1:
Change in x as x+∆x and y as y+∆y
$$Y+∆y=fx+∆x.....(b)$$ Step-2:
Subtract (a) and (b):
$$∆y=f(x+∆x)-f(x)$$ Step-3:
Find rate of change ?
Divide both sides by ∆x
$$\frac{∆y}{∆x}=f(x+∆x)-\frac{f(x)}{∆x}$$ Step-4:
We cannot say like that ∆x is 0 and but here we make it that it approach towards zero And we write it as dx
$$∆x→dx$$
$$\text{Here}\;∆x=dx$$$$\text{Here}\;∆y=dy$$
$$\frac{dy}{dx}\;=\;f(x+dx)-\frac{f(x)}{dx}$$
Lets apply on function:
$$f(x)=x^3$$
Step-1:
$$f(x+ dx)=(x+dx)^3$$
Step-2:
$$(x+dx)^3= x^3+3x^2dx+3x(dx)^2+(dx)^3$$
Step-3:
We know the slope formula:
$$\frac{dy}{dx}=\lim\limits_{x \to 0}f(x+dx)-\frac{f(x)}{dx}$$ Step-4:
Just put values:
$$\frac{dy}{dx}=\lim\limits_{x \to 0}\frac{(x^3+3x^2dx+3x(dx)^2+(dx)^3-x^3)}{dx}$$ Step-5:
Simplify:
$$=\lim\limits_{x \to 0}\frac{(3x^2dx+3x(dx)^2+(dx)^3)}{dx}$$ $$=\lim\limits_{x \to 0}\frac{dx(3x^2+3x(dx)+(dx)^2)}{dx}$$ Step-5:
divide by dx
$$=\lim\limits_{x \to 0}(3x^2+3x(dx)+(dx)^2)$$ Step-6:
Now dx tends towards zero which means apply limits
$$\frac{dy}{dx}=3x^2$$