To keep things simple and easy, we study one more case
$$\frac{d^2y}{dx^2}+P\frac{dy}{dx}+qy=f(x)$$
Fact: Where p and q are constant and f(x)≠0. The complete solution to such an equation can be found by combining two type of solution
-
The general solution of homogeneous equation:
$$\frac{d^2y}{dx^2}+P\frac{dy}{dx}+qy=0$$
-
Particular solution of non homogeneous equation:
$$\frac{d^2y}{dx^2}+P\frac{dy}{dx}+qy=f(x)$$
Note that f(x) could be a single function or a sum of two or more functions.
Fact: This method depends on Integration
The problem with this method is that , although it may reach at a solution , in some cases, the solution are in form of integral
Begin with general solution
On introduction to Second Order Differential Equation we learn how to find the general solution.
$$\frac{d^2y}{dx^2}+P\frac{dy}{dx}+qy=0$$
And reduce it to the characteristic equation:
$$r^2+pr+q=0$$
Which is a quadratic equation that has three possible solution types depending on the discriminant
$$p^2-4q$$
Where
$$p^2-4q$$
is
Positive:
We get on two real roots, and the solution is
$$y=Ae^{y_1x}+Bx^{y_2x}$$
Zero:
We get one real roots, and the solution is
$$y=Ae^{yx}+Bx^{yx}$$
Negative:
We get two complex roots
$$r_1=v+wi$$
and
$$r_1=v+wj$$
,and solution is
$$y=e^{vx}(Ccos(wx)+iDsin(wx))$$
The fundamental solution of the equation
In all three cases above “y” is made of two part:
-
$$y=Ae^{y_1x}+Be^{y_2x}$$
is made of
$$y_1=Ae^{y_1x}$$
and
$$y_2=Be^{y_2x}$$
-
$$y=Ae^{yx}+Bxe^{yx}$$
is made of
$$y_1=Ae^{yx}$$
and
$$y_2=Bxe^{yx}$$
-
$$y=e^{vx}(Ccos(wx)+iDsin(wx))$$
is made of
$$y_1=e^{vx}Ccos(wx$$
and
$$y_2=e^{vx}iDsin(wx))$$
y1 and y2 are know as fundamental solution of the equation 1 and y2 and are said to be linearly independent because neither function is a constant multiple of the other.
Wronksian
When W(y1 , y2) are two fundamental solutions of homogeneous differential equation as follows:
$$\frac{d^2y}{dx^2}+P\frac{dx}{dy}+Qy=0$$
Then wronskian W(y1 , y2) is a determinant of a matrix.
$$E.g\;=\; \begin{matrix} y_1 & y^2 \\ y'_1 & y'_2 \\ \end{matrix} $$
$$=y_1y'_2-y_2y'_1$$
$$|W(y_1,y_2)|\;\neq\;0$$
for linearly independent
$$|W(y_1,y_2)|\;=\;0$$
for linearly dependent
The Particular Solution
By using the wronskian we can also find particular solution of homogeneous differential equation
$$\frac{d^2y}{dx^2}+P\frac{dx}{dy}+Qy=f(x)$$
Formula:
$$y_p(x)=-y_1(x)\int\frac{y_2(x)f(x)}{W(y_1,y_2)}dx+y_2(x)\int\frac{y_1(x)f(x)}{W(y_1,y_2)}dx$$
Example:
$$\frac{d^2y}{dx^2}-\frac{3dy}{dx}+2y=e^{3x}$$
Solution:
-
Step#1: we will find general solution
The characteristics equation is:
$$r^2-3r+2=0$$
Factors:
$$(r-1)(r-2)=0$$
$$r=1$$
$$r=2$$
So,we have general solution of given differential equation:
$$y=Ae^x+Be^{ex}$$
Here, fundamentals solutions and their derivatives are
$$y_1(x)=e^x$$
$$y'_1(x)=e^x$$
$$y_2(x)=e^x$$
$$y'_2(x)=e^x$$
-
Step#2: We will find wronskian
$$y=Ae^x+Be^{2x}$$
$$w(y_1,y_2)=y_1y'_2=y_2y'_1$$
$$2e^{3x}-e6{3x}$$
-
Step#3: We will find the particular solution by using
$$y_p(x)=-y_1(x)\int\frac{y_2(x)f(x)}{W(y_1,y_2)}dx+y_2(x)\int\frac{y_1(x)f(x)}{W(y_1,y_2)}dx$$
-
Step#4: First,we try to solve the integral:
$$\int\frac{y_2(x)f(x)}{w(y_1,y_2)}$$
$$\int\frac{e^{ex}e^{3x}}{e^{3x}}dx$$
$$\int\;e^{2x}dx$$
$$\frac{1}{2}e^{2x}$$
Then
$$y_2(x)\int\frac{y_1(x)f(x)}{w(y_1,y_2)}dx\;=e^{2x}e^x=e^{3x}$$
$$\int\frac{e^xe^{3x}}{e^{3x}}dx$$
$$\int\;e^xdx$$
$$e^x$$
$$-\frac{1}{2}e^{3x}$$
Here also:
$$y_2(x)\int\frac{y_1(x)f(x)}{w(y_1,y_2)}dx$$
$$\int\frac{e^xe^{3x}}{e^{3x}}dx$$
$$\int\;e^xdx$$
$$=e^x$$
Then
$$y_2(x)\int\frac{y_1(x)f(x)}{w(y_1,y_2)}dx=e^{2x}e^x=e^{3x}$$
Lastly
$$y_p(x)=-y_1(x)\int\frac{y_2(x)f(x)}{W(y_1,y_2)}dx+y_2(x)\int\frac{y_1(x)f(x)}{W(y_1,y_2)}dx$$
$$-\frac{1}{2}e^{3x}+e^{3x}$$
$$\frac{1}{2}e^{3x}$$
Complete solution of differential equation is:
$$y=Ae^x+Be^{2x}+\frac{1}{2}e^{3x}$$
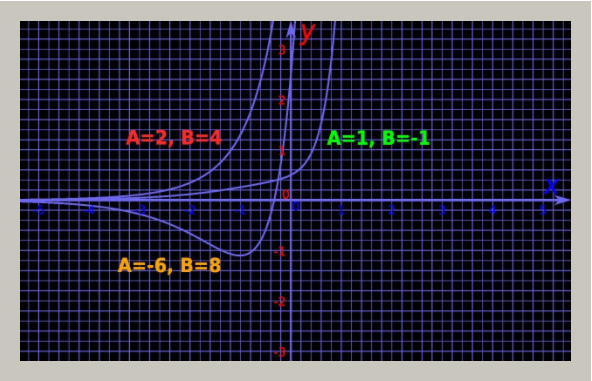
Similar to graph given below (example values of A and B):