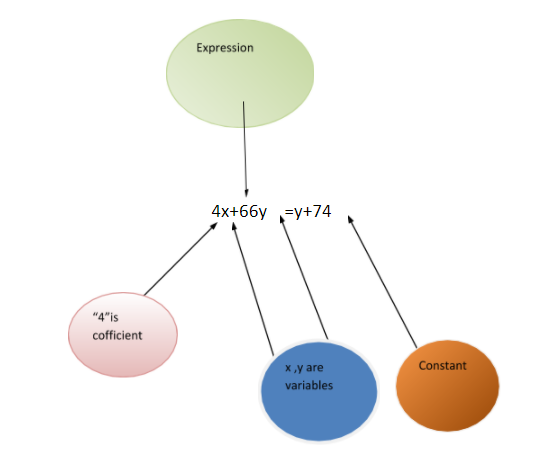
Concept of Variable, Constant, Expression, Cofficient
Differential Calculus
Functions:
It is a special type of relationship in which we give values as input and which gives result as output.
Example:
$$B=x^3$$
or
$$y=f(x)$$
Function should have Specific Name: A function has a specific name and also some function has no name then we have to give name(as f and many other of your choice) to them to make function useable.
Example of function with no name:
$$B=x^3$$
Parts of function
- The input
- The relationship
- The output
Function Representation:
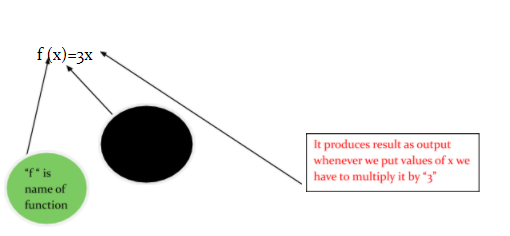
How to read Functions
$$y=f(x)$$
Here we read function as y as a function of “x”
Here y is use as dependent variable(depend on x) and x is independent variable.
When we give value to x (input) we have answer in y(output).
Formal Definition:
A function basically describe relation (one and only one) between elements of two sets
$$F(x)= x^3$$
function of cube
$$F(1)=1$$
mean putting value x in function as we put x as input we have output 1
$$F(2)=8$$
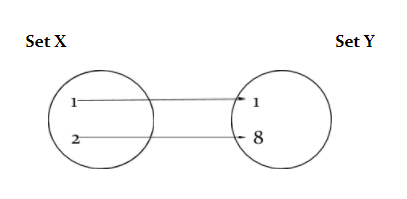
Let
$$F:X \rightarrow Y$$
is a function from set X to Y here the Set X is called Domain and Set Y is called Range of a function
So, Range of
$$f(x)={1,2}$$ $$Domain of f(x)={1,8}$$
Types of Function
- Algebraic Function: $$y=x2+1$$
-
Trigonometric Functions:
y = sinx or cosx or tanx or secx or cotx or cosecx
graph
-
Exponential Functions:
$$y=e^2x$$ -
Logarithmic Functions
$$y=a^x$$Then,
$$x=log Y a$$where a>0
-
Explicit Functions:
When we express y as function of “x”
$$x^2+1-y=0$$ $$y=x^2+1$$ -
Implicit Functions:
When y cannot be expression as function of “x”
$$x^2+1-xy=5$$