Continuity of Function
A function is said to be continuous if it has no breakable graph
Graphical Representation:
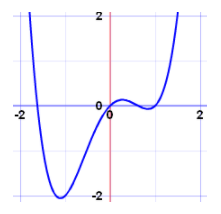
Fact: Here you can see the graph has no breaks or holes in it which means it is a continuous function and it also shows there is no missing point between values.
Question: What does discontinuity mean then?
Answer: It shows holes or breaks in the graph.
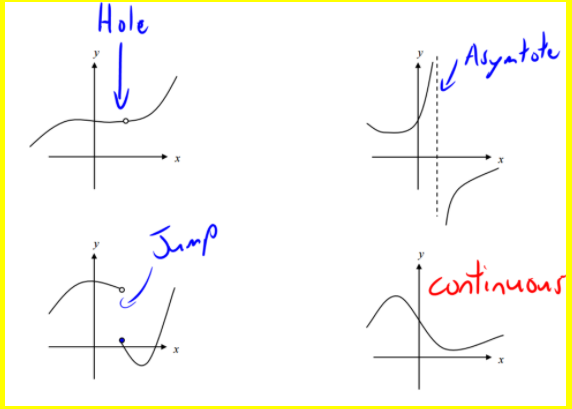
Discontinuous Function
A type of function which has not continuous graph which indicates hole or break in graph
Few Quick Review:
-
As,there is hole and jump so these are discontinuous function
-
Asymptote also show discontinuity of function
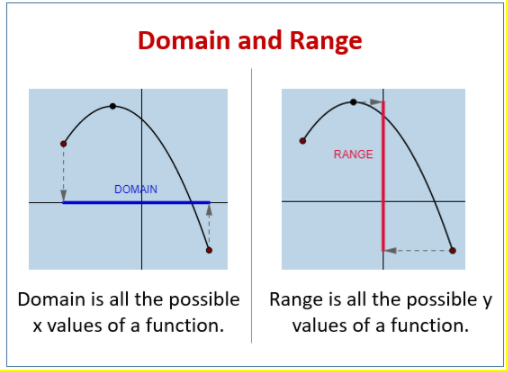
Domain of Function
Domain and range are two important portion in functions
Example:
$$\frac{1}{x3-1}$$
$$\text{When}\;x=1$$
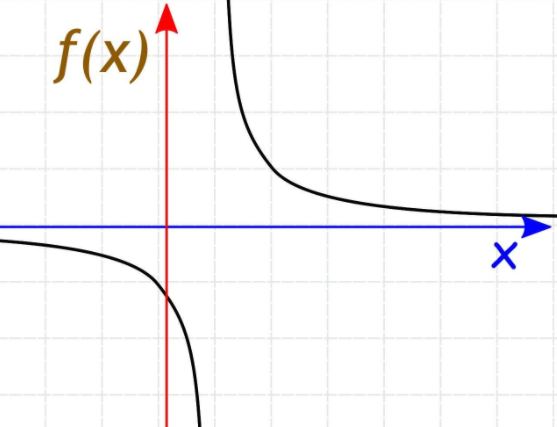
$$\frac{1}{x3-1}=\frac{1}{0}=\text{undefined}$$
So,we can say that this function is discontinuous at x=1
So
$$F(x)=\frac{1}{x3-1}$$
is not continuous(discontinuous) at every real number.
Let us change domain to x>1
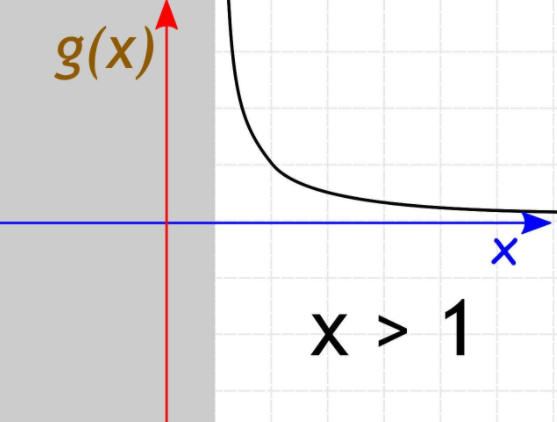
So ,here g(x) is continuous also it does not contain the value of x=1 so it is continuous
Fact: If a function is continuous in its domain is called continuous function.
Formal Definition of continuity of function
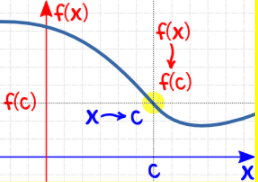
A function is said to be continuous at x=a if
- If f(x) is defined
- $$\lim\limits_{x \to a}f(x)=f(a)$$
- The limit of f(x) is f(c) as x approaches to a
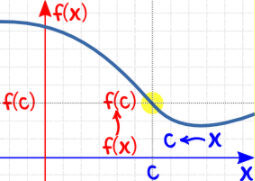
Limit from both sides:
-
If limit of left hand side
≠ to limit of right hand side so limit does not exist
- And this is true for every value of a in its domain
Make Sure two things, For every value of x:
- F(x) should be defined
- And limit at x should be equal to f(x)
Examples:
Let
$$fx=\frac{x^4-1}{x-1}$$
for all real numbers
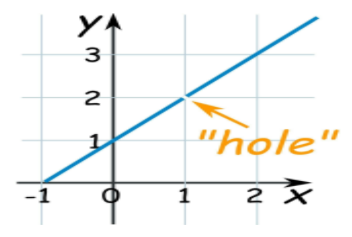
Solutions:
The function at x=1 is not defined
$$fx=\frac{x^4-1}{x-1}=\frac{0}{0}$$
So,it is continuous function as point( 1) f(x) should be defined is not satisfied
let take x<1 then so now fx does not contain x=1 so now it is continuous at x<1 (does not have hole or break)
Piecewise Function
A type of function in which we often use more than one formula for defining the output and each output has its own domain
f(x)=formula 1 if x is in domain1 formula 2 if x is in domain 2
Example of Piecewise Function
g(x)={3 if x ≤ 1 x if x>
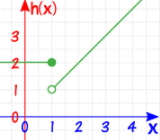
Since, it is defined when x=1 as g(1)=3 (no break)
Also, at x=1 you can’t say like that what is limit of function as there are two points:
- 3 from left side
- 1 from right side
So,the limit does not exist at x=1 as there is a break in the graph so we can say that function is not continuous which means it is discontinuous.
Example:
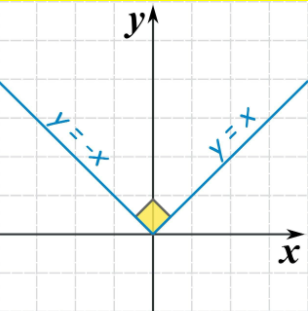
The absolute value function in piecewise notation:
|x|=[x if x≥0 -x if x<0]
Evaluation in Piecewise-Defined Function:
$$F(x)=8x+3$$
where x ≤ 0
=8x+6 where x ≥ 0
Evaluate the following:
- F(-1)
- F(3)
f(x) is defined on as 8x+3 for x=-1 as -1<0
$$f(-1)=8(-1)+3=-5$$
f(x) is defined on 8x+6 for x=3 as 3≥0
$$f(3)=8(3)+6$$
$$=30$$