Slope of a Function

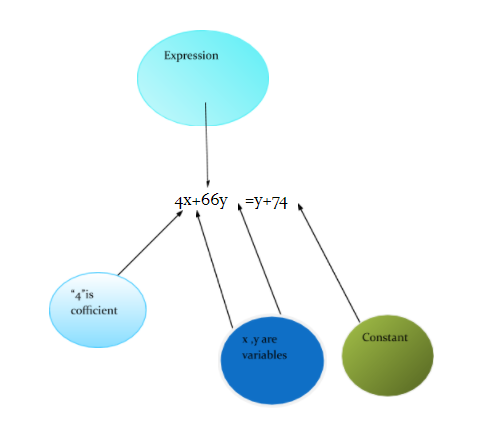
Concept of Variable, Constant, Expression and Coefficient

Differential Calculus

Functions

It is a special type of relationship in which we give values as input and which gives results as output.

Example: $$B=x^3$$

or

$$y=f(x)$$

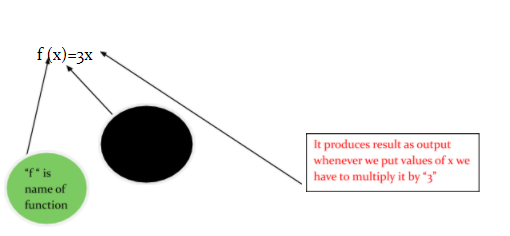
Function should have Specific Name: A function has a specific name and also some function has no name then we have to give name(as f and many other of your choice) to them to make the function usable.

Example of function with no name:

$$B=x^3$$

Parts of function

1. The input
2. The relationship
3. The output

Function Representation:

How to read Functions

$$y=f(x)$$

Here we read function as y as a function of “x”

Here y is use as dependent variable(depend on x) and x is independent variable.

When we give value to x (input) we have answer in y(output).

Formal Definition:

A function basically describe relation (one and only one) between elements of two sets

$$F(x)= x^3$$

function of cube

$$F(1)=1$$

mean putting value x in function as we put x as input we have output 1

$$F(2)=8$$

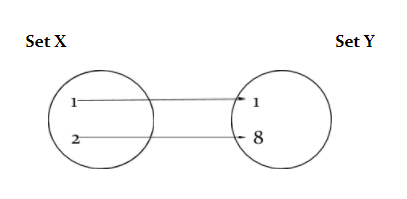
Let

$$F:X \rightarrow Y$$

is a function from set X to Y here the Set X is called Domain and Set Y is called Range of a function

So, Range of

$$f(x)={1,2}$$ $$Domain of f(x)={1,8}$$

Types of Function

1. Algebraic Function: $$y=x2+1$$

2. Trigonometric Functions:

   y = sinx or cosx or tanx or secx or cotx or cosecx

   graph

3. Exponential Functions:

   $$y=e^2x$$

4. Logarithmic Functions

   $$y=a^x$$

   Then,

   $$x=log Y a$$

   where a>0

5. Explicit Functions:

   When we express y as function of “x”

   $$x^2+1-y=0$$ $$y=x^2+1$$

6. Implicit Functions:

   When y cannot be expression as function of “x”

   $$x^2+1-xy=5$$

Slope of function

Differential and Integral Calculus are opposite to each other, very same to the process of multiplication and division, but we will talk about that later.

Dave uses differential calculus to divide time and distance into small pieces to reach at exact answer

So, Dave’s answer to question was by chance will it apply for other functions:

Lets try for

$$y=x^2$$

This is very same to previous example and it will slope on graph and there is no thought of jump for this one as we have talk before

Example:

Find Slope of function at x=1 where f(x)= y=x²

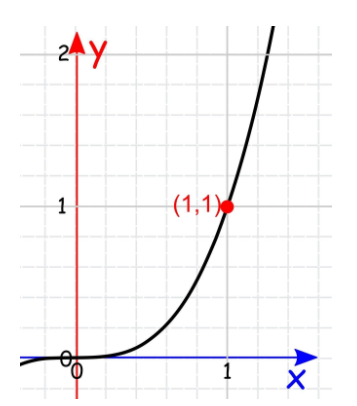
At x=1 ,y=s(1)²=1

At

$$x=1+∆x$$ $$y=(1+∆x)^2$$

By solving

$$=(1+∆x)^2$$

$$Y=1+2∆x+(∆x)^2$$

Difference between the value of y from x=1 to x=1+∆x:

Difference in

$$y=1+2∆x+(∆x)^2-1$$

Difference in

$$y=2∆x+(∆x)^2$$

Finding slope:

$$Slope=\frac{2∆x}{∆x}+\frac{(∆x)^2}{∆x}$$

So , when ∆x approach towards 0 so

Slope =2

So,graph of y=x²

Slope is changing constantly but at the point (1,1) we draw tangent line which is parallel to x –axis is a slope = 2

Slope of Function

Use this interesting method to find solve slope at point,given instruction below.

Instruction:

Put your function in box and your function will be live plotted there

Now move point A to B in function line.When they are near to each other they will move to function

Taking point A and B close to the point to find slope at that particular point Also,when A and B are on top to each other the slope at that point anything

So keep them at a small distance apart.

Now zoom fit by pressing “Yes”

Now take the point near together again

Keep zooming and moves the point near till you are satisfied with an answer

This is an idea about differential calculus and we cannot have gap between values and slope can be any value but as gap approach towards zero,the slope head towards true slope at that point

Find Slope

$$Y=e^x$$

• For x=1
• For x=2

There is only few hundred pixel in each direction,so the calculation are not totally exact but you should give good what is feel what is going on

And don’t worry you can use differential calculus to get accurate answer