
The word Calculus mean small pebble, As, it is like something by looking at its small pieces or parts.
Definition: It is all about changes
Invented By: NEWTON, LEIBNIZ in 70s
Differential Calculus
Here we divide problem into small parts then find solution. We also use differential calculus to find to steepness of a curve. In short, it tells how rapidly something changes.
Integral: It is all about how things are combining
Integral Calculus: It is basically used to find area under the curve and here we combine small pieces or parts of problem and then find how much change there.
Example: Downloading a movie
Introduction to Calculus

John and Steve are traveling in a bike, but the speedometer is damaged due to some technical issue.
Steve: Listen, John what is our current speed?
John: Hang on for a minute...
Well, in the last minute we have traveled 1.4km so we are going at speed 1.4km/min x 60 minutes in an hour=84 km/h
Steve: I don’t want average speed and I am interested to know the current speed in the last minute?
John: Let ,we measure our current speed at this traffic sign now

So, at this traffic sign for a 0 second and distance is also 0 meters!
Here speed is 0m/0s=0/0=I don’t know it actually
I am unable to measure it as Steve! as I need some of the value of distance and time to calculate it and as you have said time is zero so how we can measure it?
This is quiet intresting,you think that its easy to find speed of bike at any point in time and it is not easy as you think.
Every speedometer of bike show the average speed of car at the recent last period of time.
What about getting so close
But our story is not completed yet!
John and Steve get out of bike, because they have arrived at their destination.
John is going to do some stunt with bike:
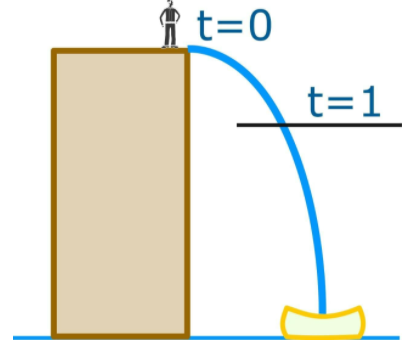
John will jump from a building of 30m
Steve, As cameraman ask. How quick you will fall after 2 seconds?
John uses this evaluated formula to find the distance to ground
$$d=5t^2$$
d=distance when fall from height
-
distance always measured in metres
t=time for jump to ground.
-
Time always measured in seconds
Here this formula is evaluated form things fall with gravity:
$$d=\frac{1}{2}gt^2$$
Example
Here at 2 second the when John fall to ground=5(2)2=20m
But, how quick is that we know that:
$$\text{Speed}=\frac{\text{distance}}{\text{time}}$$
So, at 2 sec:
$$\text{Speed}=\frac{d}{t}$$
$$\text{Speed}=\text{5m}{1s}=5ms^{-1}$$
But, Steve again, said that it is average speed since you begin to jump, I am willing to know speed at 2 sec so I have set the camera properly.
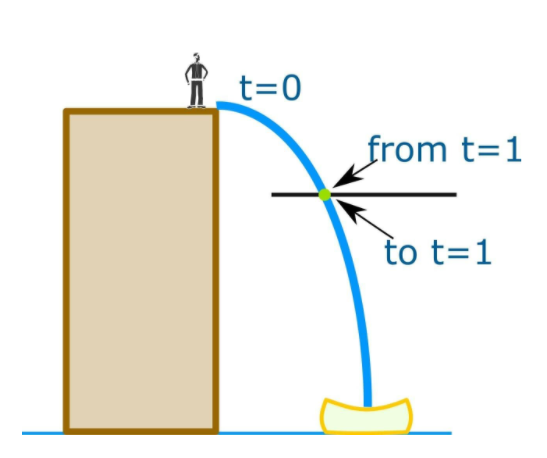
At 2 seconds the exact speed is
$$\text{Speed}=5-\frac{5m}{1}-1s=\frac{0m}{0s}=?$$
So, again John has an issue
Lets talk about that how do we calculate speed at an exact movement of time?
What is time period and what is the distance travelled by a bike?
They are both null and which means we have to nothing find
But John has an idea, imagine a time even short doesn’t matter
John has not give this time a particular value John name it as:
∆t which is known as del t and John calculate the distance changing
From t to ∆t+t.
At 2 sec John has jump:
using
$$5t^2$$
$$5(2)^2=20$$
At (2+∆t) John has jump=5x(2+∆t)2
We can Simplfy as:
(2+∆t)2=(2+∆t)(2+∆t)
=(∆t)2+4∆t+4
So, at (2+∆t) John has jump
d=5x(2+∆t)2m
d=5x((∆t)2+4∆t+4)
d=20+5(∆t)2m+20∆t
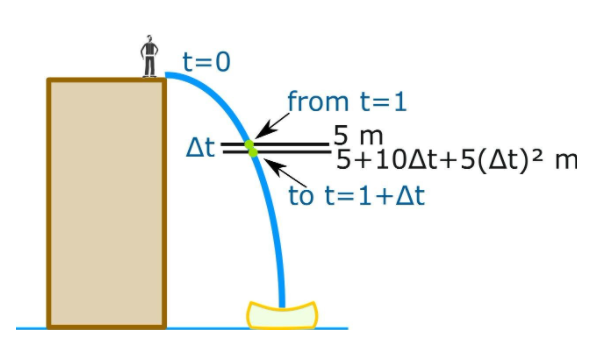
Facts: When time is 2 seconds=d=20m
When time is( 2+∆t)2 seconds
d=20+5(∆t)2m+20∆t
So the difference between 2 seconds and (2+∆t)2 seconds we have
Change in d = 20+5(∆t)2m+20∆t-20m
Change is distance/time
Speed=20+5(∆t)2m+20∆t-20m/∆ts
Speed=5∆tm/s+20 m/s
Now, the speed is 5∆t2+20∆t m/s so John take the value of ∆t=0 So ,we have
Speed=20 m/s
Hurrah! John get an answer
John:I will be falling at speed of 20m/s
Steve:I thought said you will not calculate it
John:That was my approach before calculus
Yes, no doubt,that was use of Calculus